Replacing Coulombs with Meters

Although we owe respect to the pioneers of physics, including Coulomb, Newton, Ampere, Tesla and more, one of the issues that causes a separation of the electrical domain and mechanical domain of physics is that these physicists were honored by using their names for the units of matter and electromagnetic properties. By having a system with numerous units, the average student is not inclined to dive into the details of the true meaning of each property.

Simplification of Units

Most of the units that have been given honorary names can indeed be derived in SI units to become simpler. For example, amperes can be derived to C/s, which is Coulombs per second. For the student that explores it to this level of detail, he or she would understand that it is the flow of charge in a given timeframe.

Yet, there is one unit that is misunderstood and its meaning can simplify many other units. More importantly, its simplification can bridge the gap between the mechanical domain (measured in properties of mass) and the electrical domain (measured in properties of charge). The unit is charge, which is measured in Coulombs. By replacing Coulombs with the units of distance (meters), the following are examples of units that are simplified:

Amperes becomes a velocity
Voltage becomes a force
Inductance becomes a mass

And there are many more units from electromagnetism that can now be expressed in units that are described with phrases from mechanical systems. An illustration of one of the derivations when C is replaced with m is voltage. Its units are the same as force:

$V_{units} = \frac{kg(m^2)}{s^2(C)} = \frac{kg(m)}{s^2}$

Consolidation of Mechanical and Electrical Domains

But the simplification of units is just the start of what can be accomplished with the simple change of Coulombs to meters. Newton’s laws of motion and gravity use mass as the property to describe the forces of large objects. Coulomb’s law uses charge as the property to describe the forces of particles. The two cannot be reconciled when one has the property of mass and the other has charge. However, when charge is considered a distance, mass and charge can be related and the equations can be reconciled.

To relate mass and charge, Coulombs can be explained as wave amplitude, which is measured as a distance (meters). If one assumes a substance in the vacuum of space that has a physical property of kilograms, and moves as waves, then the following are descriptions of mass and charge:

Mass is standing longitudinal wave energy (without consideration of wave speed – c²)
Charge is traveling longitudinal wave energy over distance (force)

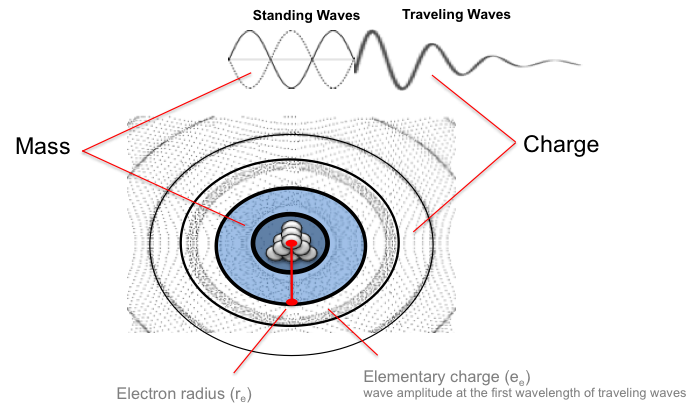
The elementary charge of a single particle (e_e) is the wave amplitude at the first traveling wavelength. Amplitude is the average displacement from equilibrium of the substance, hereafter referred to as granules. The displacement of granules will be greater near the electron’s core and decrease in amplitude at distance, as granules collide and transfer energy to more granules as it spreads spherically.

Because matter (measured as rest energy or mass) is formed from the same wave that has electrical properties (measured as charge), they can be related both logically and mathematically. Logically, it is simply the type of longitudinal wave: standing or traveling. A standing wave is stored energy. A traveling wave, by definition, is traveling energy. A photon, by comparison, is a different wave form – it is a transverse wave in which wave propagation is perpendicular to particle motion (versus longitudinal which is in the direction of motion).

Proof of the Relation of Matter and Charge

The energy of the wave can be described classically in the following equation. Since it is a wave it can be expressed in true wave format – wave speed, wavelength and wave amplitude (see energywavetheory.com). However, for the purpose of using terms familiar to modern physics, the classical form is used:

$E = \frac{\mu_0 c^2}{4 \pi}\bigg(\frac{qq}{r}\bigg)$

Mass is the stored energy of standing waves within the electron’s radius (r_e). Therefore, it is the energy equation without consideration of wave speed (c²).

$m= \frac{E}{c^2}$

For a single electron, the charge (q) is the elementary charge (e_e).

$q = e_e$

Using the CODATA values for these fundamental physical constants and solving for mass, it derives to the electron’s mass.

$m_e = \frac{\mu_0}{4 \pi} = 9.109x10^{-31} (kg)$

Charge is wave amplitude at a given distance (r). It can be expressed as energy, but it is often expressed as a force, known as Coulomb’s law. Force is energy at a distance.

$F = \frac{E}{r}$

The Coulomb constant is the magnetic constant times wave speed squared, over 4p. Coulomb gave it the letter k.

$k = \frac{\mu_0 c^2}{4 \pi}$

Substituting the Coulomb constant for the constants in the energy equation (above), and then substituting it into the force equation (by adding another r in the denominator), yields Coulomb’s law.

$F = k \bigg( \frac{qq}{r^2} \bigg)$

Logically, both mass and charge can be explained as waves. And mathematically, the electron’s mass can now be expressed in terms of charge (q/e_e), relating the domains of mechanical and electrical by equation.

About the Author

Jeff Yee

Social Media:

Mind Blown: Greatly simplifies the Standard Model and its number of free variables

Profession: VP, Innovation & Partnerships at ZTE

Interest: Continue developing the Energy Wave Theory